Если ты дочитал до этого урока – ты молодец! Инвестиции – тема нелегкая для новичка: много терминов и страшных слов. И даже несмотря на то, что этот курс создавался с расчетом на начинающих, без сложных деталей и терминов не обошлось. Поэтому спешим обрадовать – это последняя сложная тема в курсе. Финальный босс. Поэтому сохранись на чекпоинте, налей еще чайку и поехали дальше. Тема сложная, но очень важная.
Ты можешь спросить: если я все правильно понял, то с инвестициями могу рассчитывать на 5–15% доходности в год? Это же так мало? Как можно на этом разбогатеть?
Ответ: используя Сложный процент.
Посмотри, как менялось состояние Уоррена Баффета. Может показаться, что до 50 лет с ним как будто ничего и не происходило. На самом деле единица измерения на графике – миллиарды долларов. Понятно, что и до 50 лет Баффет был далеко не бедным человеком, но суммы эти настолько незначительны по сравнению с нынешним состоянием, что на графике их почти не видно:
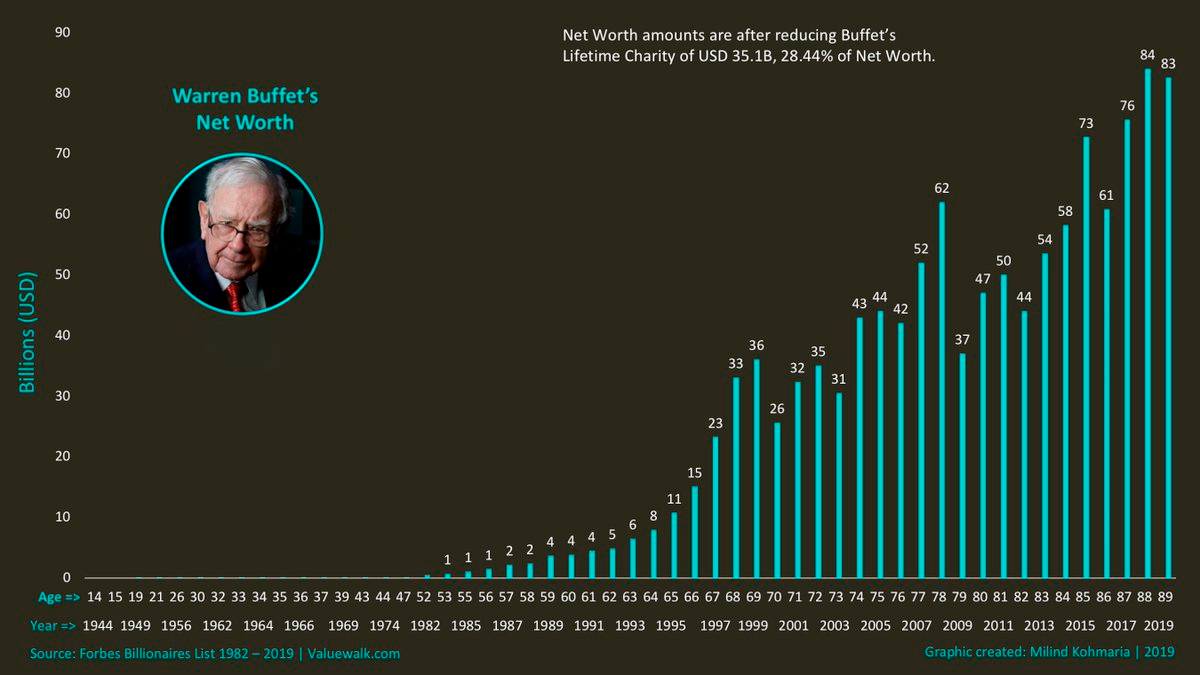
Да, настоящий рост у миллиардера начался только после 50 лет. В чём причина? В эффекте сложного процента.
Сложный процент – это когда проценты начисляются на проценты, которые начислены на проценты, которые начислены на предыдущие проценты… и так до бесконечности. От того он и Сложный.
Если отобразить эффект сложного процента в виде графика, то мы получим:
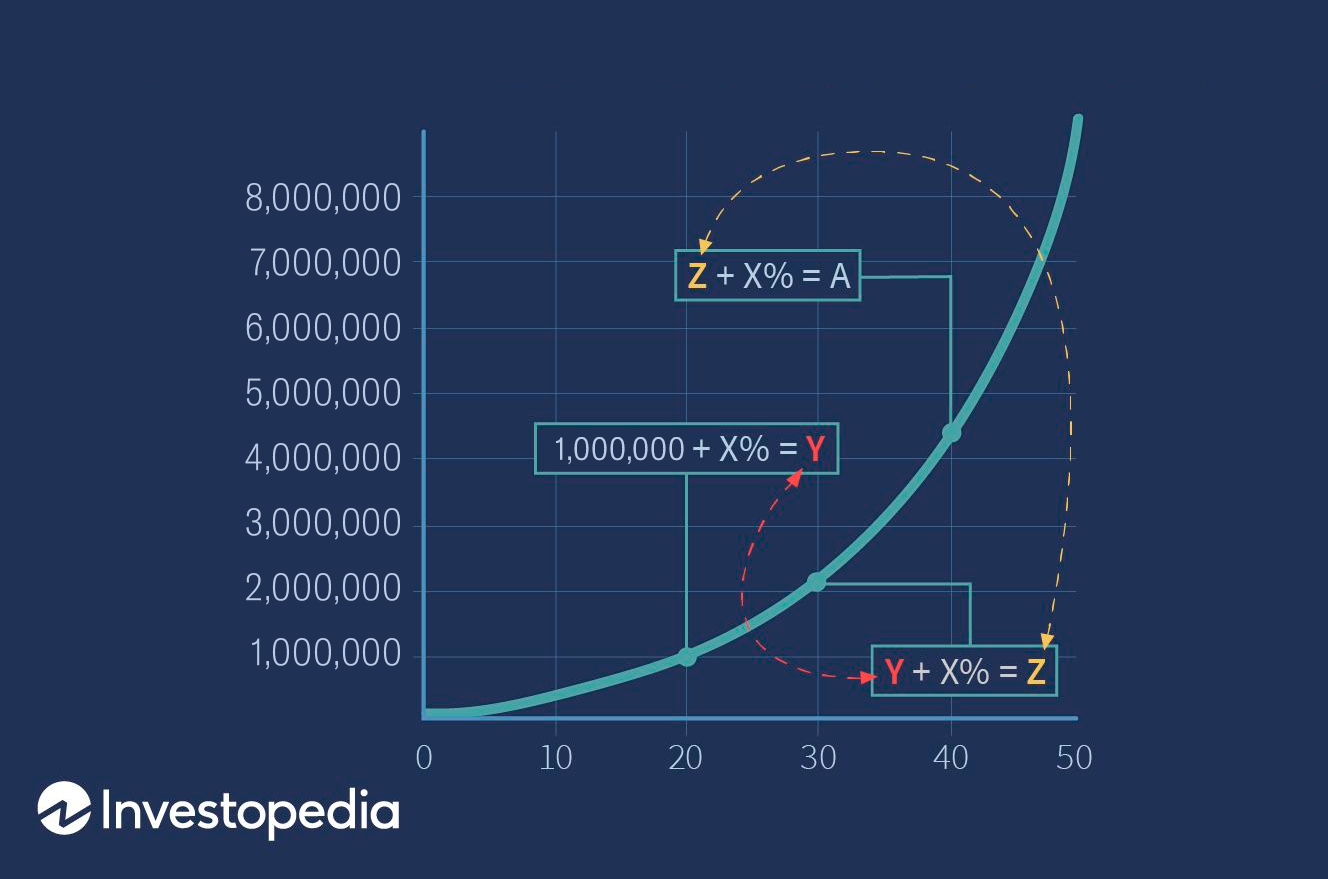
В начале временного отрезка рост минимальный. Но с течением времени рост становится экспоненциальным.
Почему так происходит?
Это можно сравнить с эффектом снежного кома – snowball effect. Снежок увеличивается за счет площади соприкосновения со снежной поверхностью. Чем больше эта площадь, тем больше нового снега прилипнет. Если мы представим снежок, который катится по бесконечно длинному и гладкому снежному склону, то в самом начале площадь соприкосновения будет очень мала. Но вот он прокатился вниз по склону, постепенно увеличиваясь в диаметре. Через какое-то время, он уже больше метра в обхвате.
Что стало с его площадью соприкосновения?
Она стала еще больше, а значит к ней липнет больше снега.
Таким образом, снежок увеличивается в размерах не линейно, а по экспоненте. К его размерам с каждым оборотом не прибавляется один фиксированный объем снега. С каждым оборотом сама сумма увеличения становится все больше и больше.
Это и есть сложный процент.
Теперь давай в цифрах.
Предположим, в первый год твои инвестиции выросли на 10%. Было $1000, а стало $1100. Но в следующем году, при этих 10%, сумма увеличится уже не на $100, а на $110. Вроде бы разница небольшая, но всё равно круто – процент остался тот же, а сумма увеличилась. Через год 10% превратятся уже в $121. Ещё через год – в $132. И так до бесконечности.
Да, 10% от условных $1000 – это немного. Но эти же 10% с $1 млн – это уже $100,000.
Эффекту сложного процента, требуется время, чтобы разогнаться. И вот тут то и кроются две основные проблемы:
Первая – мы молоды и хотим всё сразу. Желательно побольше и как можно скорее. Потому что мы живем сейчас. 10% в год – это так мало, а до 60 лет так долго ждать. Зачем мне Феррари в 60? Я хочу его сейчас.
И вторая – человеку в целом сложно думать категориями далекого будущего. Не пойми неправильно, мы можем планировать наперед, можем представить себя в старости, хоть этого и не хочется, но очень сложно сравнивать так называемую opportunity cost (цену нашего выбора сегодня), когда речь идет о будущем. То есть, если у тебя спросят сейчас: что ты выберешь: одну пряник сейчас или 5 через час? На этот вопрос большинство ответит: 5 пряников через час.
Но, что интересно, если задать этот вопрос 3-летнему ребенку, он может и ответит, что хочет 5 пряников. Но, скорее всего, он всё равно не удержится перед соблазном съесть пряник сейчас.
Трехлетке сложно представить будущее, которое наступит даже через час. С возрастом мы учимся оценивать свои возможности намного лучше и можем заглядывать в будущее намного дальше. Но как насчет будущего через 30 лет? Вот с этим уже сложней.
Вот тебе другой пример.
Курильщик понимает, что курение сокращает жизнь. Согласно исследованиям, начав курить в 20, ты сокращаешь жизнь на 14 лет. Казалось бы, 14 лет – это много, поэтому сделать выбор и бросить пагубную привычку – логичное решение. Но человеку сложно заглядывать настолько далеко перед. Сейчас-то все нормально.
Но эти две проблемы можно решить, если сделать несколько ментальных упражнений.
Начнем с первой проблемы, про Феррари в 60 лет.
Ну, во-первых, и в 60 лет Феррари – это круто. Во-вторых, нужно понимать, что наши дедушки и бабушки в 60–70 уже были (или есть) теми, кого мы называем стариками. Но вот что удивительно, наши родители, приближаясь к 60, выглядят моложе. Язык не поворачивается назвать их стариками. И если у поколения наших дедушек и бабушек продолжительность жизни была в среднем 60–70 лет, то у наших родителей это уже 80–90. До скольки доживем мы? Ученые говорят, что, учитывая улучшение образа жизни, глобальные тренды на ЗОЖ, развитие медицины, мы спокойно проживем больше 90 лет. А наши дети проживут уже более 100 лет.
Поэтому мы с тобой в 60 лет, скорее всего, будем еще очень даже живчиками. Да, мы будем ворчать на молодежь и говорить что «в наше время было лучше», но в полной мере сможем насладится поездкой на Феррари.
Поэтому можно сделать такой вывод: у нас достаточно времени в запасе, чтобы эффект снежного кома достиг по-настоящему больших объемов.
Теперь ко второй проблеме.
Неспособность заглядывать далеко вперед – это уже посложнее. Но опять таки, нам в Казахстане с этим чуть проще. И поможет нам в этом одна простая мысль – у нас попросту нет вариантов. В текущих условиях лучше не рассчитывать на будущую пенсию.
Какой будет курс валют через 30 лет? Сколько будут стоить обычные вещи, не говоря уже о билетах на Мачу Пикчу?
В 60 лет денежный поток в виде заработной платы прекратится. И чем мы тогда будем заправлять свой Феррари? Только личными накоплениями и инвестициями.
Итак, давай вернемся к сложному проценту и продолжим изучать его внимательней и под разными углами.
Мозгу сложно понять, что такое экспоненциальный рост из-за сложного процента. Ведь на словах вроде бы всё просто, но на деле, поверь мне, мозгу сложно мыслить такими категориями. Поэтому вот ещё один пример.
Ты, наверное, слышал притчу о человеке, который придумал шахматы и в качестве награды попросил рис. Если нет, то вот история:
Дело было в Индии. Султану Шераму так понравились шахматы, игра, которую придумал изобретатель по имени Сета, что он предложил тому любую награду. Сета сказал, что в качестве награды возьмет рис. Он попросил положить одно зернышко риса на первую клетку шахматной доски. На вторую клетку – два зернышка, на третью клетку – четыре зернышка, на четвертую – восемь зернышек. И так далее. То есть каждая новая клетка содержала в два раза больше риса, чем предыдущая.
Султан был оскорблен. Он предложил изобретателю любые богатства, а тот попросил немного риса. Ну что за идиот? На утро султан спросил, получил ли дуралей свои несколько мешков зерна? На что услышал, что такого количества зерна попросту не существует в мире. Не говоря уже про запасы царства.
Так сколько же в итоге Сета должен был получить зерна?
Ответ: 2 в 63 степени. Или вот столько зерен – 9,223,372,036,854,775,808.
Мы даже не знаем как прочесть это число. Девять дофигаллиардов?
Если посчитать вес такого количества риса, то получится 1.2 триллиарда метрических тонн. Что в 1 645 раз больше, чем мировое годовое производство риса сегодня.
Эта история – наглядный пример работы сложного процента.
Теперь переведем это на деньги. В данном случае каждая новая клетка - это условно год, а удвоение суммы - это 100% доходности в год. Если заменить рис на доллары, а клетки на годы, то уже к 21-му году из $1 получится $1 млн. В жизни, естественно, стабильная 100% доходность каждый год – нереальная штука. Но доходность, скажем, в 10% вполне реальна.
При этом начинать инвестировать можно не с $1, как в примере выше. К тому же, если инвестировать не раз в год, а каждый месяц, например, по 10% от зарплаты, сложный процент будет работать еще эффективнее.
Давай разберем силу сложного процента, уже на реальных цифрах.
Предположим, что вместо того, чтобы купить себе машину, ты начал инвестировать с какой-то суммы. Например, с $10,000. Через год к этой сумме прибавляется условный доход в 10%. Через год ещё 10%. И так далее. Механику работу сложного процента мы уже объяснили, давай наложем ее на наши цифры, распишем всё это, и сделаем таблицу на 30 лет, после ты сам увидишь, в чем сила.
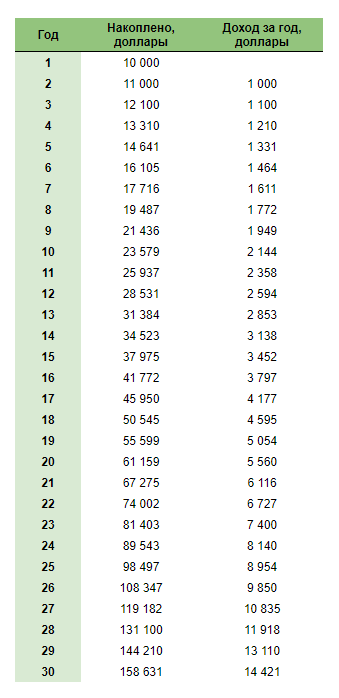
Обрати внимание, что условия не меняются, по прежнему один календарный год и доходность в 10%. Но в первый год доход по инвестициям будет $1,000, а на 30-м году это будет уже $14,421. Итог: ты вложил $10,000, и, по сути ничего не делая, превратил их в $150,000. Это то, что различные финансовые коучи называют «пусть деньги работают на тебя, а не ты на них».
Заметь, этот подсчет сделан по фиксированной сумме, то есть ты не докладываешь никаких дополнительных денег и исчисление идет по годам.
Теперь давай рассмотрим другой сценарий. Там где ты на протяжении 30 лет откладываешь ежемесячно по $100 и таким образом позволяешь сложному проценту работать не по годам, а по месяцам. 30 лет – это 360 месяцев. Средняя месячная доходность будет равна примерно 0.9%. Это чтобы за год показатель был равен примерно тем же 10%.
В таблице будет 360 строк, поэтому всю таблицу приводить не будем. Но вот первые и последние 12 месяцев получается вот такими:

В этом сценарии важно отметить следующее: во первых, в первом месяце твой доход всего $90. Но в последнем, при тех же условиях - $4 600. Во вторых, все, что ты отложил, это начальные $10,000 плюс 360 месяцев умноженные на $100, в сумме $46,000. Все остальное – почти полмиллиона долларов – это работа сложного процента.
Представь, что получится, если ты будешь откладывать не $100, а сумму, которая будет расти с каждым годом? Например с 20 до 25 лет ты можешь позволить себе откладывать лишь $100. Далее до 30 это может быть $150. После $200 и больше.
Представь как отработает сложный процент, в таком случае, в горизонте 30 лет!
Уорреном Баффетом конечно так не стать, но выйти на пенсию долларовым миллионером - вполне возможно. Баффет, в отличие от нас, понял, как работает сложный процент, ещё в 14 лет. Примерно тогда же он и начал инвестировать. Поэтому к 30 годам у него уже был первый миллион долларов. По сегодняшним меркам это около $10 млн.
Так что повторить успехи дяди Баффетта получится у единиц. Для этого понадобится полное погружение в мир инвестиций и десятилетия опыта.
Но ведь не обязательно становиться таким же богатым как он. Главное подумать о своем будущем, о будущем своих детей, и после – вооружиться таким же терпением и систематично вкладывать деньги в ценные бумаги.
Итак, давай подытожим:
Сложный процент – это то, что позволяет делать огромные состояния, если у тебя хватит терпения. Это про черепаху, которая обгоняет зайца. Сложному проценту нужно время, чтобы разогнаться, но когда он это сделает, его уже не остановить. Нам очень сложно и на самом деле вообще не хочется думать о будущем, тем более о настолько далеком будущем, но чем раньше ты об этом задумаешься, тем больше у тебя будет времени, чтобы разогнать сложный процент. Ведь все большое - начинается с малого. Никогда не рано об этом подумать. Начни закладывать фундамент в беззаботное финансовое будущее уже сейчас.




















